Bilangan Berpangkat Dan Bentuk Akar Kelas 9 – BAB 1
Perpangkatan bilangan
Contoh :
-
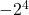 = -(2x2x2x2) = -16
= -(2x2x2x2) = -16 -
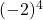 = - 2x - 2x - 2x - 2 = 16
= - 2x - 2x - 2x - 2 = 16
Sifat – sifat berlaku pada bilangan berpangkat
Contoh :
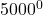 = 1
= 1- Sederhanakan bentuk dari
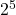 x
x 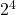 !
!
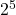 x
x 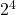 =
= 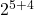 =
= 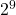
- Sederhanakan bentuk dari
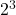 :
: 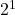 !
!
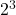 :
: 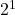 =
= 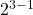 =
= 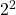
- Sederhanakan bentuk dari
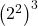 !
!
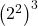 =
= 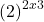 =
= 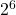
- Nilai dari
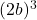 !
!
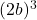 =
= 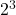 x
x 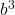 =
= 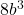
- Tentukan nilai dari
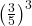 !
!
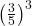 =
= 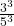 =
= 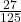
- Tentukan nilai dari
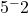 !
!
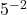 =
= 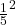 =
= 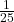
Bentuk baku bilangan
Contoh :
- 1200000 = 1,2 x
- 0,000056 = 5,6 x
- 4356,78 = 4,35678 x
Persamaan pangkat sederhana
Contoh :
![]() = 27
= 27
![]() =
= ![]()
![]() – 1 = 3
– 1 = 3
![]() = 3 + 1
= 3 + 1
![]() = 4
= 4
Sifat – sifat bentuk akar
Contoh :
- 2
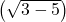 = …
= …
=
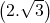 +
+ 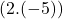 =
= 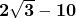
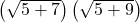 = ….
= ….
=
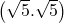 +
+ 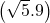 +
+ 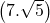 + (7.9)
=
+ (7.9)
= 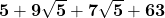 =
= 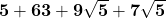 =
= 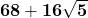
-
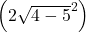 = …
= …
=
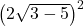 =
= 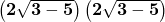 =
= 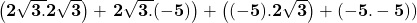 =
=  =
= 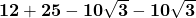 =
= 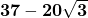
- 10
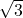 : 2
: 2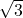 = 5
= 5
Merasionalkan Penyebut Pecahan Bentuk Akar
=
=
=
x
=
=
x
=
=
x
=
=
x
=
Contoh :
Rasionalkan penyebut pecahan berikut:
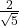 = …
= …
=
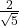 x
x 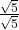 =
= 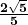
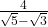 = …
= …
=
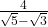 x
x 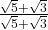 =
= 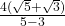 =
= 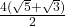 =
= 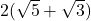
Menyederhanakan Bentuk 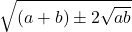
Contoh :
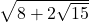 = …
= …
=
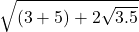 =
= 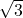 +
+ 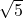
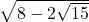 = …
= …
=
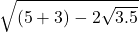 =
= 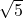 -
-